(Gesamt-)Inhaltsverzeichnis

Eigenverbrauch und seine Berechnung

Wer privat eine PV-Anlage betreibt, möchte möglichst viel von ihrem Ertrag auch selbst verbrauchen, und zwar am besten direkt. Überschüssigen Strom in einer Batterie für spätere Nutzung zwischenzuspeichern ist technisch aufwendig, teuer und mit zusätzlichen Verlusten behaftet.

Der Eigenverbrauch über einen gegebenen Zeitraum bestimmt sich als Integral (bzw. näherungsweise als Riemann-Summe) über

min(PV-Leistung(t) + Speicher-Entnahmeleistung(t), Haushaltslast(t))

wobei PV-Leistung(t) die im Zeitpunkt t vom Wechselrichter abgegebene Leistung ist, Speicher-Entnahmeleistung(t) die einem ggf. vorhandenen Speicher entnommene Leistung (gemessen ebenfalls am Ausgang des jeweiligen Wechselrichters) und Haushaltslast(t) die im Zeitpunkt t insgesamt vom Haushalt benötigte Leistung.
Meist kann man die Haushaltslast nicht direkt messen, weil Wechselrichter üblicherweise hinter dem Messpunkt für die Gesamt-Strommessung einspeisen. Weil erzeugte oder einem Speicher entnommene Leistung dann mit umgekehrten Vorzeichen in den Leistungssaldo am Unterverteiler eingeht, errechnet sich die Last

ohne Speicher und bei DC-gekoppeltem Speicher als Summe aus dem Gesamt-Leistungssaldo am Unterverteiler und der Ausgangsleistung des Wechselrichters, bzw.
bei AC-gekoppeltem Speicher als Summe aus Gesamt-Leistungssaldo, Ausgangsleistung des PV-Wechselrichters und Ausgangsleistung des Batterie-Wechselrichters, abzüglich Eingangsleistung des Ladegeräts.

Wenn die Daten eines Zweirichtungszählers vorliegen, lässt sich der Eigenverbrauch einfach durch die Differenz aus PV-Nettoertrag (+ ggf. einem Speicher entnommene Energie) und extern eingespeister Energie berechnen.

Der direkte (nicht ggf. über einen Speicher erhöhte) PV-Eigenverbrauch ergibt sich, wenn in der Berechnung die Speicher-Entnahme durch 0 ersetzt wird.

Der nicht selbst genutzte Anteil, also die — stets nicht-negative — Differenz aus PV-Leistung (+ Speicher-Entnahmeleistung) und davon selbst verwendeter Leistung, wird meist ins externe Netz eingespeist. Bei Steckersolargeräten geschieht dies ohne Vergütung, aber auch wenn man selbst erzeugten Strom als Kleinunternehmer verkauft, hat man zusätzliche Bürokratie und bekommt ziemlich wenig heraus.

Ökonomisches Ziel ist also, den Eigenverbrauchsanteil zu maximieren. Der Eigenverbrauchsanteil (Nutzungsgrad) ist der Anteil der Netto-Stromerzeugung, der direkt verbraucht wird (oder ggf. nach gewissen Verlusten über einen Speicher). Je höher er ist, desto weniger Energie wird ins externe Stromnetz eingespeist. Je kleiner die Anlage ist, umso leichter kann man eine hohe Eigenverbrauchsquote erreichen, allerdings dann bei entsprechend kleinerem Stromvolumen.

Damit verwandt ist der Eigendeckungsanteil (Selbstversorgungsgrad), also der Anteil des Eigenverbrauchs (ggf. mit Batterieentladung abzüglich Ladeverlusten) am Gesamtverbrauch. Je höher er ist, desto weniger Energie muss von extern bezogen werden. Er wird oft auch als Autarkiegrad bezeichnet, was etwas irreführend ist, denn typischerweise arbeitet der Wechselrichter der PV-Anlage auch dann nicht ohne Verbindung zum Netzstrom, wenn gerade kein Netzbezug (also Stromfluss von außen) stattfindet. Je größer die Anlage ist, umso höher fällt der Autarkiegrad aus, allerdings oft zu Lasten des Eigendeckungsanteils. Eine Quasi-Autarkie (Eigendeckungsanteil 100%) kann man aber nur mit enormer Stromspeicher-Kapazität erreichen.

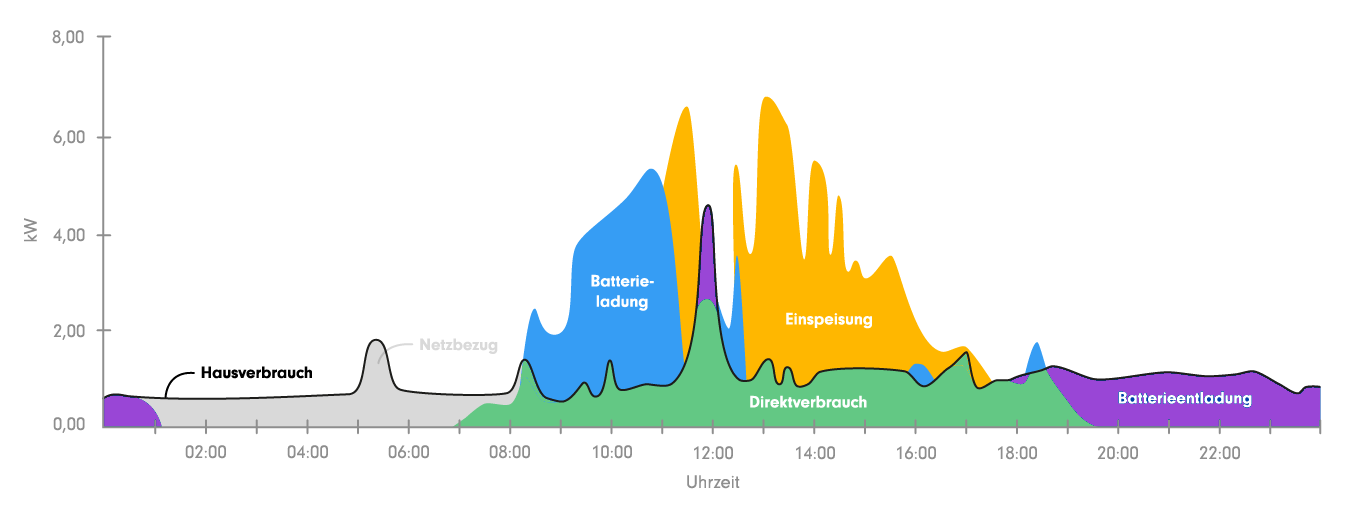Das Bild veranschaulicht den typischen Stromverlauf bei einer Hausdach-PV-Anlage mit 7kWp Nennleistung und 5kWh Stromspeicher an einem ziemlich sonnigen Tag mit mittags etwas Wolken. Weitere schöne Erklärungen mit Grafiken gibt es hier.

Typische Rentabilität kleiner PV-Anlagen

Wenn die Einsparung an Stromkosten durch eine PV-Anlage die Kosten eingeholt hat, hat sich die Anlage amortisiert, also die Investition kaufmännisch gelohnt. Die Investition rentiert sich im Verhältnis der Jahres-Ersparnis zu den Kosten.

Wie eingangs geschrieben kann man bei optimaler Platzierung von Solarmodulen pro Jahr etwa 1,1 kWh Strommenge pro Wp installierter Solarleistung gewinnen. Rechnen wir beispielsweise mit einer Investition für die PV-Anlage von 0,55€/Wp (inklusive anteiliger Kosten für Wechselrichter, Montage, Reparatur, etc.), dann ergeben sich einmalige Kosten von 0,5€ pro kWh Jahresertrag.
Nehmen wir für die folgenden Beispiele zudem an, dass der sog. Arbeitspreis, also die Kosten für vom Stromanbieter bezogenen Strom, 30 ct/kWh beträgt. Dann spart man also 0,30€ für jede kWh Strom, die von der PV-Anlage produziert wird und die man auch selbst verbraucht, statt sie von außen einzukaufen.
Anfang 2023 fiel in Deutschland die Mehrwertsteuer für die Komponenten kleiner privaten PV-Anlagen weg, aber auch die Strompreise sanken im Frühjahr wieder auf etwa 30 ct/kWh. Außerdem wurden PV-Module und Mikrowechselrichter durch ein globales Überangebot günstiger, so dass man Steckersolargeräte mit über 800 Wp inzwischen für unter 400€ bekommt.

Eine Balkonanlage mit 850 Wp Nennleistung kann einen Jahres-Bruttoertrag von etwa 1080 kWh erreichen, was bei 86% Gesamtsystem-Wirkungsgrad ca. 935 kWh Netto-Ertrag (Einspeisung des Wechselrichters) pro Jahr bedeutet. Wenn wir mit Kosten von 0,55€/Wp rechnen, ergibt das für diese Anlage 467,50€.

Falls man den erzeugten PV-Strom komplett selbst verbraucht, was aber praktisch kaum der Fall sein wird, ergäbe sich eine Einsparung von 280€ pro Jahr und somit eine Amortisation der Investition in nur 20 Monaten. Die Rendite würde in diesem Fall satte 60% betragen.
Bei einem durchschnittlichen Haushalts-Nutzungsprofil und Jahresverbrauch von 3000 kWh liegt der selbst genutzte Ertrag bei etwa 620 kWh pro Jahr. Der Eigenverbrauchsanteil liegt also bei 67% des Nettoertrags (und der Eigendeckungsanteil bei 21% des Verbrauchs).
Damit werden bei 30 ct/kWh Arbeitspreis jährlich 186€ eingespart. Für die Investition von 467,50€ ergibt sich eine Amortisationszeit von 2,5 Jahren und eine immer noch ausgezeichnete Rendite von 40%.

Bei einem hohen Jahresverbrauch von 6000 kWh können durchschnittlich sogar 800 kWh im Jahr (also 86% des Nettoertrags) selbst genutzt werden.

Bei geringem Jahresverbrauch von 1500 kWh können durchschnittlich nur 430 kWh im Jahr (also 46% des Nettoertrags) selbst genutzt werden.

Wenn bei 3000 kWh Jahresverbrauch montags bis freitags von 8 bis 16 Uhr nur eine konstante Last von 100 W anfällt, liegt der Eigenverbrauch entsprechend relativ gering bei 465 kWh im Jahr (also 50% des Nettoertrags) und die Amortisationszeit für die veranschlagten Kosten bei 3,3 Jahren.

In den beiden zuletzt genannten Fällen könnte man zwar überlegen, nur 1 PV-Modul (statt 2) zu installieren, aber dann hätte man auch langfristig weniger Nutzen, so dass das angesichts der geringen Kosten für PV-Module nicht ratsam wäre.

Für die Amortisation des energetischen Aufwands zur Herstellung einer Mini-PV-Anlage sollte man nach Angaben des DKE allerdings noch 2-3 Jahre zusätzlich rechnen. In die Gesamt-Ökobilanz einer PV-Anlage und ihrer Nutzung gehen natürlich noch weitere Effekte ein, die sich aber kaum quantifizieren lassen.

Online-Berechnung

Achtung: Die in diesem Abschnitt genannten Simulatoren setzen bei Einsatz eines Pufferspeichers eine ideale Speicherstrategie voraus. Ihre Ergebnisse gelten nicht bei Verwendung einer primitiven Regelung, wie sie für Steckersolargeräte mit Speicherbatterie typisch sind. Für diese kann aber der u.g. ‘SolBatSim’ verwendet werden.

Stecker-Solar-Simulator und Unabhängigkeitsrechner

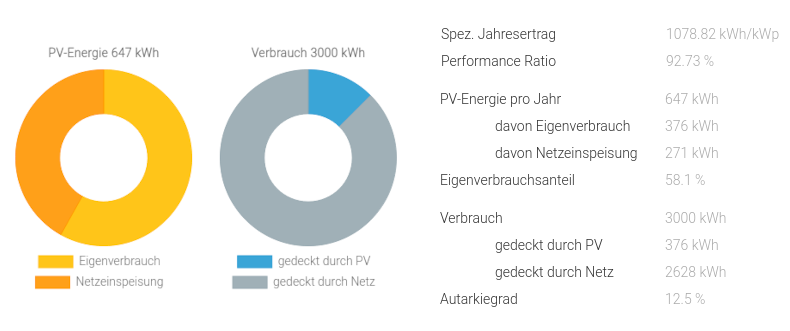
Der Eigendeckungsanteil und Eigenverbrauchsanteil lässt sich sehr einfach näherungsweise mit dem „Stecker-Solar-Simulator“ für Balkonkraftwerke bzw. dem „Unabhängigkeitsrechner“ für Hausdach-PV-Anlagen der HTW Berlin berechnen. Hier im Bild die Ausgabe bei 3000 kWh Jahres-Stromverbrauch, einem Strompreis von 40 ct/kWh und für PV-Module mit Südausrichtung, 35° Anstellwinkel (Neigung) und ohne Verschattung. 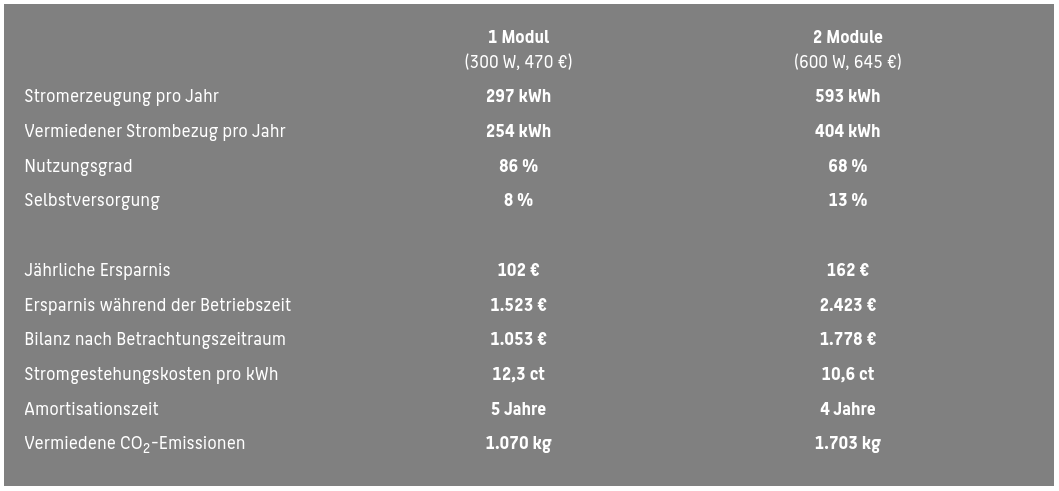Beide Simulationen nutzen intern Daten der Wetterstation Lindenberg bei Berlin aus dem Jahr 2017, in dem die Sonneneinstrahlung schwächer als normal war — für Süddeutschland kann man also gut 15% mehr PV-Leistung ansetzen. Als Eingabe verwenden sie den >Jahresstromverbrauch (mit einer typischen Lastverteilung) und die PV-Nennleistung (mit einem spezifischen PV-Jahresertrag von 1024 kWh/kWp). Man kann auch eine (nutzbare) Speicherkapazität angeben, wobei ein typischer Wirkungsgrad für LiFePO4-Batterien von 95% und typische Wandlungsverluste des Ladereglers und des Wechselrichters von jeweils 94% angenommen werden. Implizit wird eine optimale bedarfsgerechte Lade-/Entladeregelung vorausgesetzt. 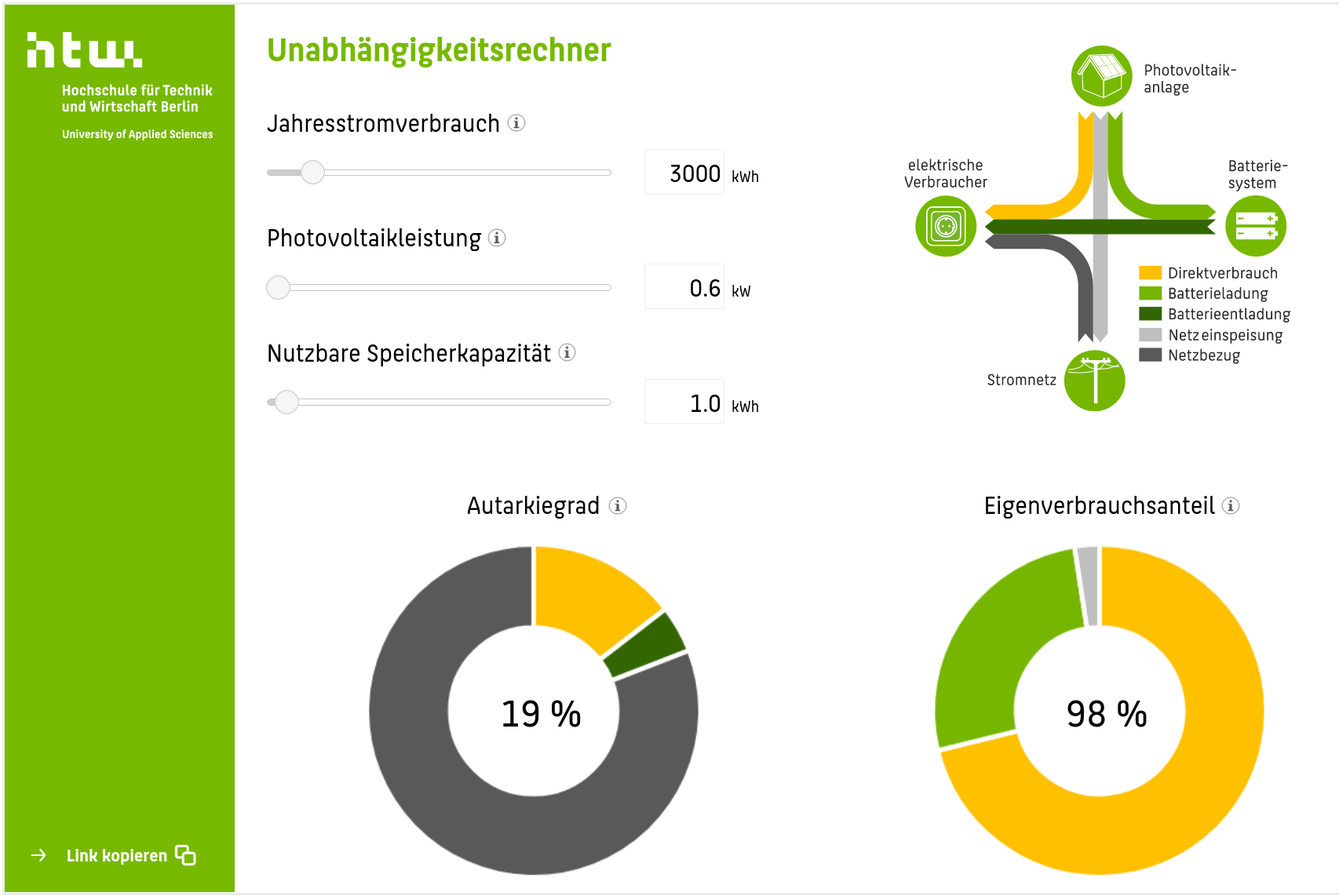Der Unabhängigkeitsrechner liefert auch den Anteil der Batterieentladung an der Stromversorgung, den man zur Ertrags- und Wirtschaftlichkeitsberechnung von PV-Speichern verwenden kann (und zwar durch Multiplikation mit dem Stromverbrauch). Für Anlagen ohne Stromspeicher sind die Ergebnisse sehr realistisch.

PV*SOL

Von der sehr soliden kommerziellen Simulationssoftware PV*SOL gibt es auch eine kostenlose Online-Variante. Auch diese ist eigentlich für große Haus-PV-Anlagen gedacht, aber wenn man beim Wechselrichter ‘TSUN’ auswählt, lässt sie sich für Balkonanlagen u.ä. verwenden, geht aber von einem für Steckersolargeräte zu hohen System-Wirkungsgrad (über 92%) aus.

Der mögliche Eigenverbrauch hängt natürlicherweise stark vom gewählten Lastprofil ab. Mit der Auswahl ‘2 Personen mit einem Kind’ bekommt man Ergebnisse, die dem von der HTW Berlin verwendeten Durchschnitt am nächsten kommen (aber etwas niedriger ausfallen).

PVTool@AkkuDoktor

Eine sehr einfache Möglichkeit, online die Amortisation zu berechnen, bietet auch das PVTool von „AkkuDoktor“. Als Besonderheit kann man hier schön sehen, wie sich Eigenverbrauchsquote, Autarkiegrad und Amortisation in Abhängigkeit von der Anwesenheit und Kapazität eines Stromspeichers ändern.

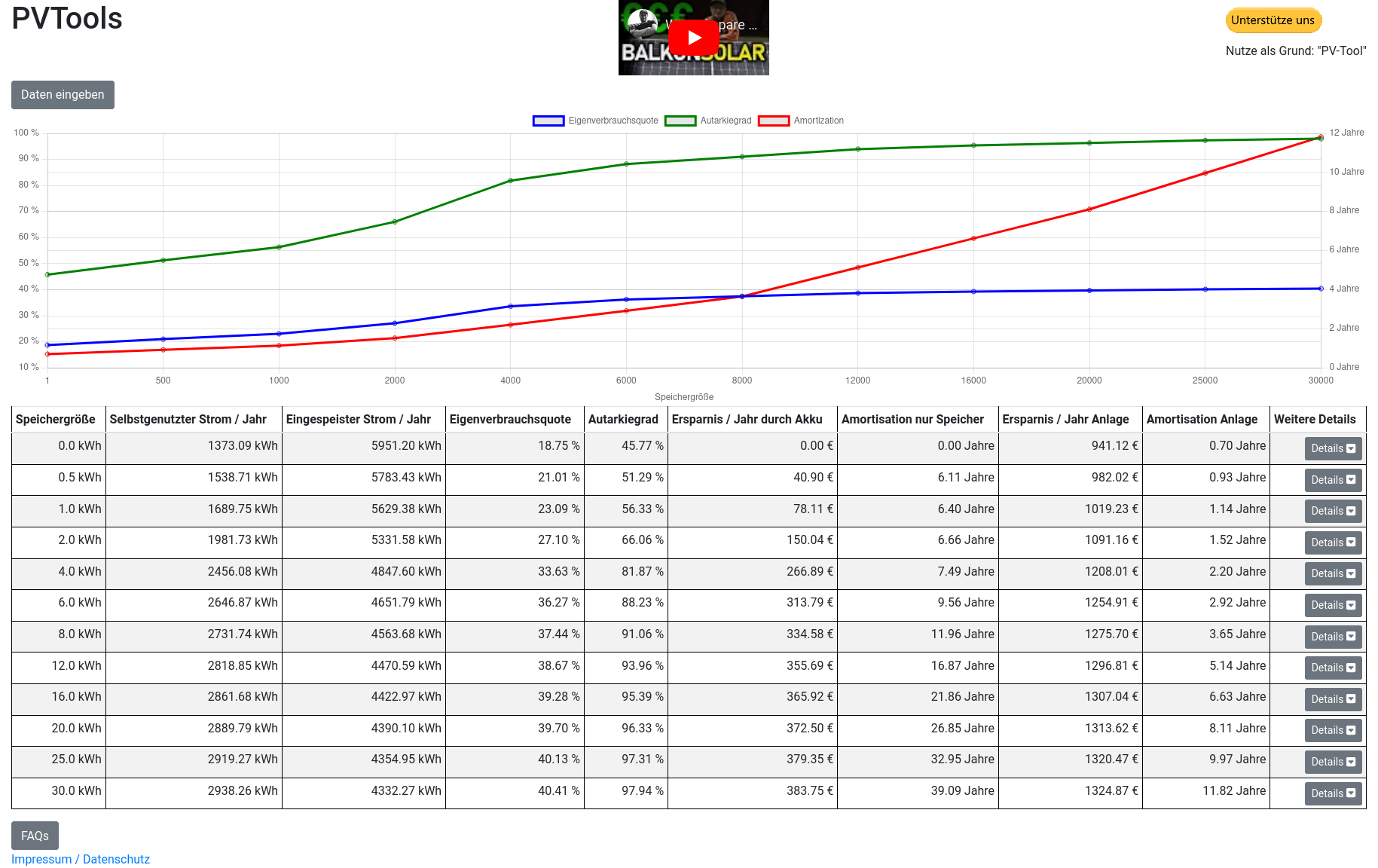Inzwischen kann man für die Simulation ein eigenes Lastprofil (allerdings nur in Stundenauflösung) hochladen und verwenden lassen.
Für Speicher wird stillschweigend eine optimale lastbasierte Lade- und Entladestrategie angenommen. Die Lade- und Entlade-Wirkungsgrade der Speicherbatterie (inkl. Verluste während der Speicherzeit) werden standardmäßig sehr hoch angenommenen: 99%. Das mag für DC-Kopplung passen, ist aber für AC-Kopplung viel zu hoch, wobei man das in den erweiterten Einstellungen anpassen kann.
Standardmäßig wird die Lade- und Entladeleistung etwas praxisfern nicht begrenzt, was sich aber ebenfalls in den erweiterten Einstellungen korrigieren lässt.

Bis Anfang Dezember 2023 waren die Simulationsergebnisse v.A. ohne Speicher und bei kleineren Speicherkapazitäten deutlich zu optimistisch. Das lag v.A. daran, dass das Standard-Haushalts-Lastprofil H0 des VDEW (inzwischen: BDEW) von 1996/97 verwendet wurde, und zwar auch nur in Stundenauflösung (statt in der verfügbaren 15-minütigen Auflösung). Damit konnten keinerlei Lastspitzen berücksichtigt werden, wozu mindestens Minutenauflösung (besser: Sekundenauflösung) benötigt wird.
Das wurde deutlich verbessert.

Stand April 2024 gibt es allerdings noch Unklarheiten z.B. bei den Wirkungsgraden, Merkwürdigkeiten wie kleine nächtliche PV-Erträge und konstante Netzbezüge und eindeutige Fehler.

brodsoft Stromverlauf

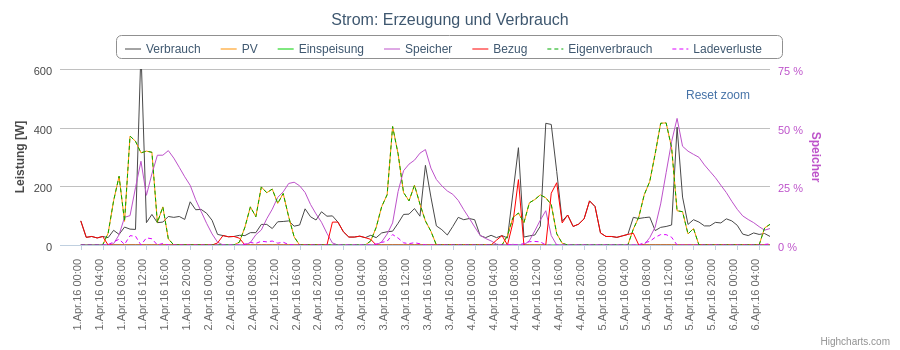Eine ältere Simulation des Eigenverbrauchs für einen gegebenen PV-Nettoertrag mit Fokus auf Stromspeicher (mit gegebener nutzbarer Kapazität und Effizienz), gibt es von brodsoft. Diese basiert auf realen Profildaten für PV-Erzeugung und Stromverbrauch, mit denen die Berechnung auf Stundenbasis erfolgt. Man kann sich in der Ausgabe auch für jeden Monat Grafiken ausgeben lassen darauf sehr schön den Verlauf der elektrischen Größen ansehen. Außerdem gibt es gute Info-Seite mit guten Erklärungen zu Eigenverbrauchsanteil und Eigendeckungsanteil zu Strategien zu ihrer Optimierung. Diese Simulation berechnet für die o.g. 600 Wp Beispiel-Anlage je nach Auswahl des Profils einen Eigenverbrauch von teils 601 kWh (Profil „allgemein 13/14“) und mehr, aber typischerweise eher 514 kWh (Profil „InGe 16“) pro Jahr.

PV Calculator

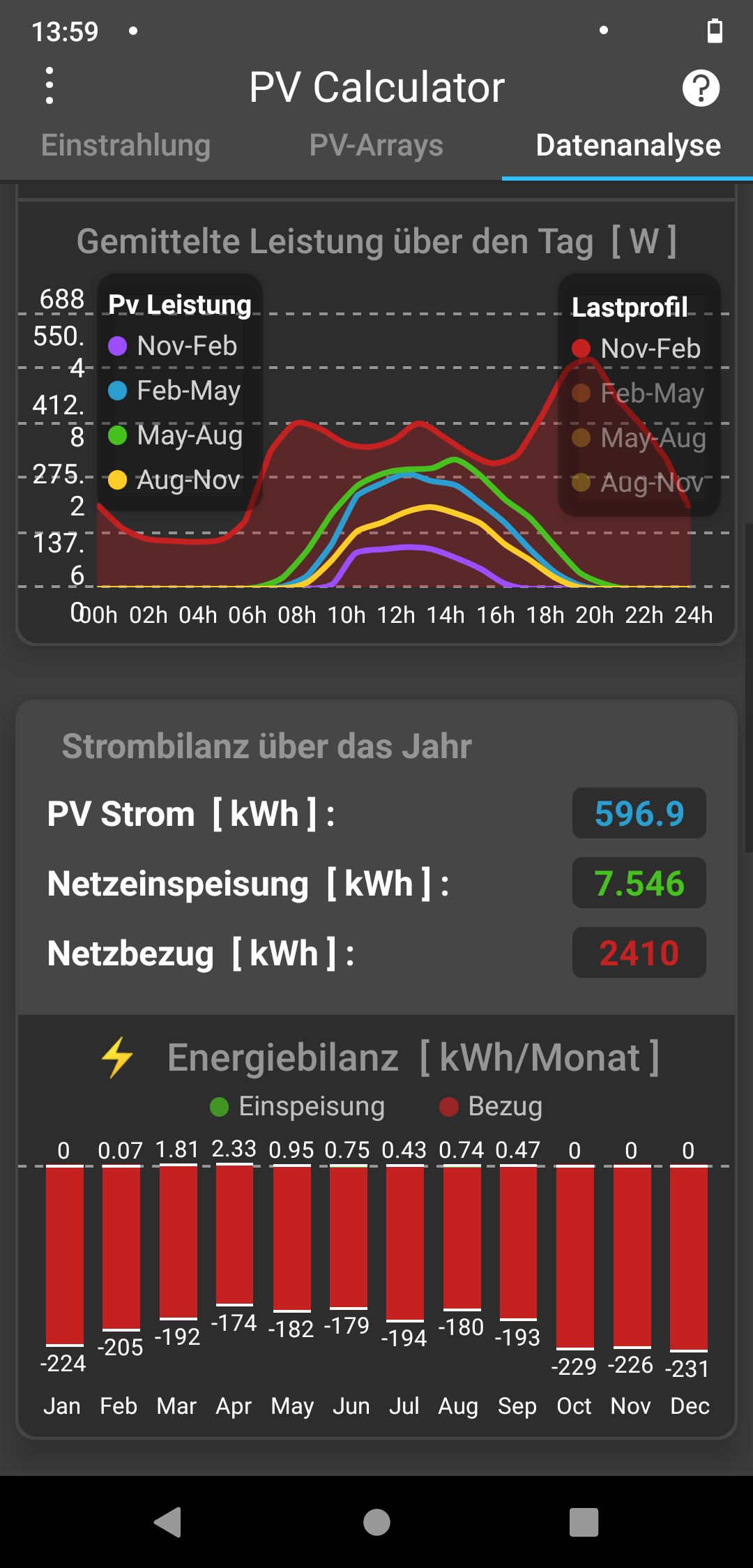
Es gibt auch eine Android-App namens PV Calculator von SusEnergy mit sehr schöner Darstellung der Ergebnisse. Sie verwendet die Daten von PVGIS und rechnet leider nur auf Stundenbasis.

Für die o.g. Beispiel-Anlage mit 850 Wp kommt sie für die gegebenen Wirkungsgrade auf einen zu geringen Jahres-Nettoertrag von 764 kWh, aber auf einen zu hohen Eigenverbrauch von 686 kWh. Das liegt teils an den angebotenen Profilen (z.B. VDEW-H0-Werktag), die eine sehr geringe zeitliche Auflösung haben und täglich die gleiche Last annehmen, wobei man in der Premium-Variante immerhin selbst welche pro Jahreszeit definieren kann. Aber das Hauptproblem ist, dass die Last nur im stundenweisen Durchschnitt betrachtet wird, also die typischen Lastspitzen unberücksichtigt bleiben. Damit ergibt sich bei 3000 kWh Jahres-Strombedarf für die meisten Profile unrealistischerweise so gut wie keine Netzeinspeisung und selbst für das Profil „Peak Morgen Abends“ eine viel zu niedrige Netzeinspeisung von 137 kWh. Außerdem wird etwas verwirrend im Gesamtergebnis nicht der resultierende Eigenverbrauch (hier 627 kWh) dargestellt, sondern der Nettoertrag und der Netzbezug.

Man kann auch Speichernutzung mit simulieren lassen, aber die Ergebnisse können schon wegen der stundenweisen Berechnung ebenfalls nicht realistisch sein.

Interessante Funktionen wie die Verwendung eigener Lastprofile und der Export der Simulationsergebnisse sind inzwischen der kostenpflichtigen Premium-Variante vorenthalten.

Ökonomisch orientierte PV-Rechner

Für die rein kaufmännische Berechnung der Rendite einer PV-Anlage und/oder Stromspeicher gibt es ein einfaches Online-Tool namens pvroi auf Englisch. Es berücksichtigt Inflation und Degradation, aber keine darüber hinausgehende Reparaturen bzw. Abschreibung. Als Ergebnis bekommt man entweder für gegebenen Preis die jährliche Rendite in % (und kann dann vergleichen, ob die Investition mehr bringt als eine andere) oder umgekehrt: Für eine Wunsch-Rendite den Maximalpreis für die Komponenten.

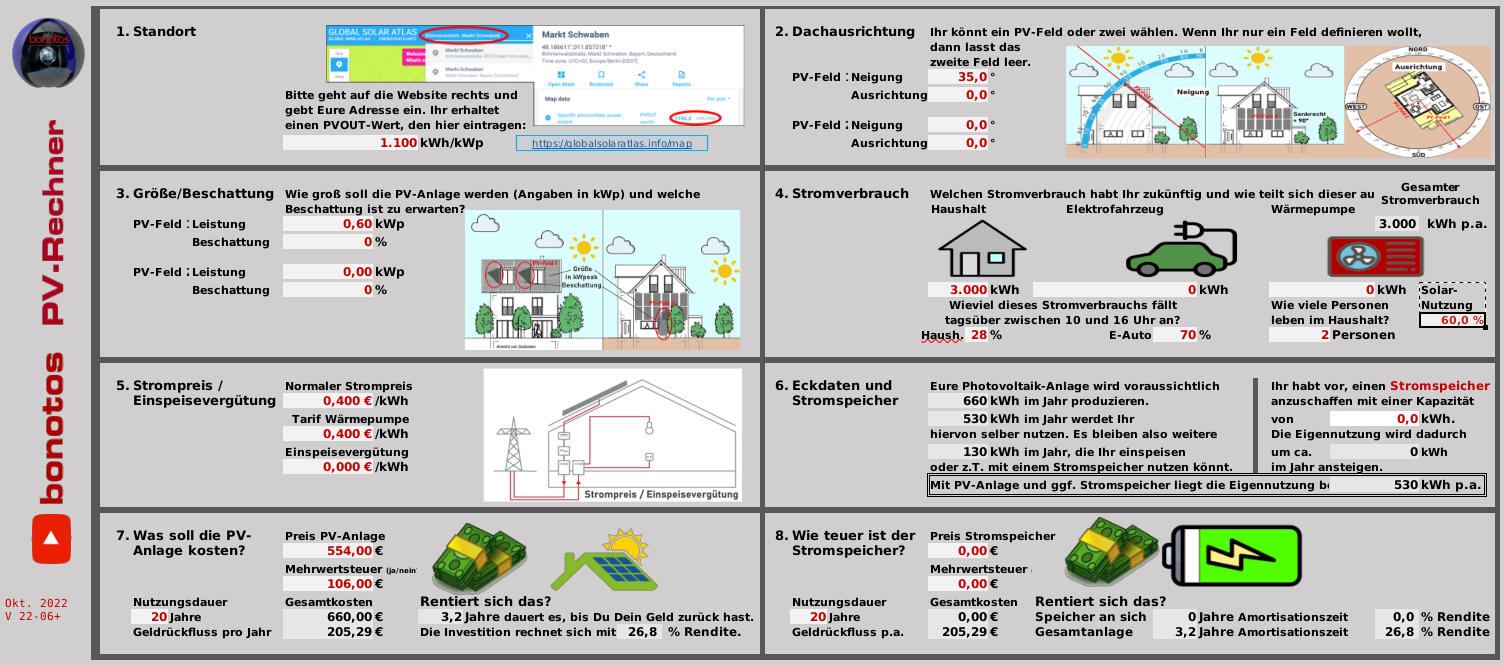
Die Offline-Tabellenkalkulation PV-Rechner hat als besonderen Schwerpunkt die kaufmännische Betrachtung inklusive Rendite und Kapitalkosten unter Berücksichtigung von Abschreibung für Reparaturen u.ä. Er ist für „große“ PV-Anlagen auf Hausdächern konzipiert, und behandelt optional gesondert das Laden eines E-Fahrzeugs, den Betrieb einer Wärmepumpe und die Nutzung eines Stromspeichers, funktioniert aber auch für Steckersolargeräte. Als Eingabe erwartet er u.A. den spezifischen PV-Jahresertrag, die Ausrichtung der Module und den geschätzten Anteil des während der Sonnenscheindauer im Haushalt nutzbaren Ertrages. Energieflüsse werden der Einfachheit halber nur grob auf Monatsbasis gerechnet, so dass wichtige tageszeitliche Effekte und Lastspitzen nicht berücksichtigt werden. Besonders die Simulation des Stromspeichers ist stark idealisiert.

Bei der o.g. typischen Balkonanlage für 660€ mit 600 Wp und 660 kWh Jahresertrag ergibt sich mit dem PV-Rechner für einen Haushalt mit 3000 kWh Jahresverbrauch, der zu 28% während der Haupt-Sonnenscheinzeiten erfolgt, ein etwas zu optimistischer Solarstrom-Eigenverbrauch von etwa 530 kWh pro Jahr. Damit könnte man bei 40 ct/kWh jährlich ca. 205€ Stromkosten einsparen, was eine Amortisationszeit von 3,2 Jahren und eine satte (Anfangs-)Rendite von 26% ergäbe.

Hinweis: Der PV-Rechner stammt von Falko (bonotos) Der originale beinhaltet auch seiner letzten Version 22-06 einen groben Fehler in der Rendite-Formel, der zu (fast) doppelt überhöhten Rendite-Zahlen führt. Ich habe mich mit Falko zu diesen und anderen Punkten ausgetauscht. Er möchte an dem Tool nichts mehr machen. So stelle ich hier eine verbesserte und etwas erweiterte Version zur Verfügung.

SolBatSim: Hochauflösende flexible Simulation

SolBatSim, ein selbst entwickelter Simulator, basiert auf Lastprofilen des Stromverbrauchs mit mindestens stündlicher, aber besser minütlicher (oder noch höherer) Auflösung. Daher und weil er die verschiedenen Arten von möglichen Verlusten differenziert berücksichtigt kommt er auf sehr realistische Ergebnisse. Aufgrund seiner großen Flexibilität deckt er fast alle üblichen Situationen ab. Aus diesen Gründen ist er auch als Referenz für andere Simulationen verwendbar.

Für die o.g. Beispiel-Anlage für den Raum München mit 600 Wp und einem PV-Nettoertrag (nach Wechselrichter-Verlusten) von etwa 662 kWh ergibt sich mit dieser Simulation unter Verwendung minutengenauer Lastprofile ohne Speicher je nach Profil ein Eigenverbrauch von ca. 460 kWh.

Das Ergebnis fällt nicht so günstig wie bei den zuvor genannten Simulationen aus, v.A. weil hier die in der Praxis relativ häufigen Lastspitzen immerhin im Minutenbereich berücksichtigt werden, die von einer Mini-Solaranlage praktisch kaum abgefangen werden können, so dass der Eigenverbrauchsanteil geringer ist als bei einer über Stunden oder gar ganze Monate gemittelten Betrachtung.

Vergleichsrechnungen auf Grundlage eines Lastprofils mit (annähernd) sekündlicher Auflösung haben ergeben, dass die Lastspitzen nur teilweise einen spürbaren Einfluss auf die Nutzbarkeit des PV-Ertrags von kleinen Anlagen haben. Bei 600 Wp sind die Eigenverbrauchs-Ergebnisse bei Lastdaten auf Stundenbasis etwa 3 bis 6% zu optimistisch, auf Minutenbasis nur bis etwa 1%.